Comprensión
de la visión de RL
Con diversos entornos, podemos
analizar, diagnosticar y editar modelos de aprendizaje por refuerzo profundo
mediante la atribución.
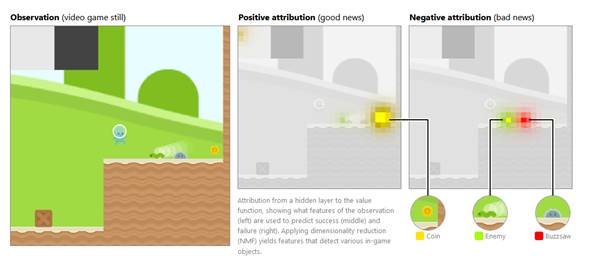
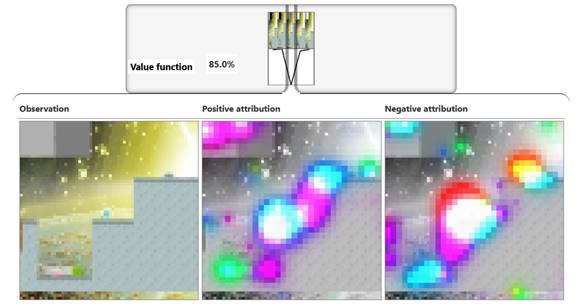
Atribución de una capa oculta
a la función de valor, que muestra qué características de la observación
(izquierda) se utilizan para predecir el éxito (medio) y el fracaso (derecha).
La aplicación de reducción de dimensionalidad (NMF) produce funciones que
detectan varios objetos en el juego.
Aprendizaje profundo por
refuerzo
El Aprendizaje profundo
por refuerzo o Deep Reinforcement Learning, es uno de los campos de investigación más prometedores
en el mundo de la Inteligencia Artificial.
¿Qué es el aprendizaje
profundo por refuerzo?
Es una nueva generación de las
técnicas de aprendizaje automático (Machine Learning),
que se caracteriza por un paso más a la evolución de la forma en que la maquina
aprende a realizar una tarea.
Los sistemas de aprendizaje
por refuerzo exploran y adquieren datos sobre el problema por propia
iniciativa, diseñando automáticamente estrategias que le den
solución.
¿Cómo funciona el aprendizaje
profundo por refuerzo?
Un sistema de aprendizaje
profundo por refuerzo está conformado por una máquina o agente inteligente que
aprende a optimizar un proceso de decisión.
Es similar a cuando entrenas a
un perro en donde le enseñas hacer las acciones por medio de recompensas o
castigos.
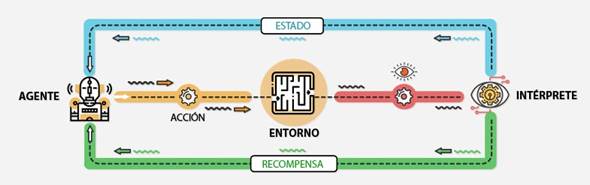
·
Agente: El alumno y el que toma
las decisiones
·
Entorno (Medio Ambiente): Donde
el agente aprende y decide que acciones realizar
·
Acción: Un conjunto de acciones
que el agente puede realizar
·
Estado: El estado de agente en
el entorno
·
Recompensa: Por cada
acción seleccionada por el agente, el entorno proporciona una recompensa. Por lo
general, un valor escalar.
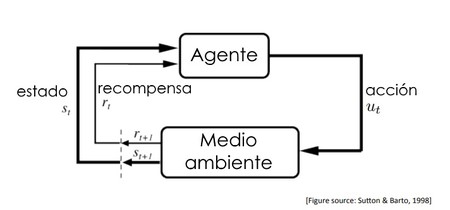
¿Cómo aprende una maquina?
Para que la maquina aprenda,
el agente interactúa con un entorno, que puede ser el proceso de decisión real
o una simulación del mismo. El agente trabaja
observando el entorno, y tomando una decisión para comprobar que efectos produce.
Si el resultado de esa
decisión es beneficioso, el agente aprende automáticamente a repetir esa
decisión en el futuro, mientras que si el resultado fuera perjudicial evitará
volver a tomar la misma decisión.
De este modo, siguiendo un
proceso de aprendizaje por condicionamiento similar al de los
seres vivos, el agente aprende qué decisiones son más adecuadas según la
situación, y desarrolla estrategias a largo plazo que maximicen los beneficios.
El cerebro o la capacidad de
aprendizaje del agente viene dada por un modelo de Deep Learning o red neuronal profunda. Esto
permite explotar todos los avances recientes en redes neuronales artificiales,
pudiendo así tratar con problemas que requieran analizar datos no estructurados
como imágenes, sonidos o lenguaje natural.
En este artículo, aplicamos
técnicas de interpretabilidad a un modelo de aprendizaje por refuerzo (RL)
entrenado para jugar al videojuego CoinRun.
Utilizando la atribución combinada con la reducción de dimensionalidad como en,
creamos una interfaz para explorar los objetos detectados por el modelo y cómo
influyen en su función y política de valor. Aprovechamos esta interfaz de
varias formas.
·
Disección del fracaso.
Realizamos un análisis paso a paso del comportamiento del agente en los casos
en los que no logró la recompensa máxima, lo que nos permite comprender qué
salió mal y por qué. Por ejemplo, un caso de falla fue causado por un obstáculo
que se ocultó temporalmente de la vista.
·
Alucinaciones.
Encontramos situaciones en las que el modelo "alucinó" una
característica que no estaba presente en la observación, lo que explica
inexactitudes en la función de valor del modelo. Fueron lo suficientemente
breves como para no afectar el comportamiento del agente.
·
Edición de modelos.
Editamos manualmente los pesos del modelo para cegar al agente a ciertos
peligros, sin cambiar el comportamiento del agente. Verificamos los efectos de
estas ediciones comprobando qué peligros hacen que fallen los nuevos agentes.
Dicha edición solo es posible gracias a nuestro análisis anterior y, por lo
tanto, proporciona una validación cuantitativa de este análisis.
Nuestros resultados dependen
de que los niveles en CoinRun se generen
procedimentalmente, lo que nos lleva a formular una hipótesis de diversidad
para la interpretabilidad. Si es correcto, entonces podemos esperar que los
modelos RL se vuelvan más interpretables a medida que los entornos en los que
se entrenan se vuelven más diversos. Proporcionamos evidencia para nuestra
hipótesis midiendo la relación entre interpretabilidad y generalización.
Finalmente, proporcionamos una
investigación exhaustiva de varias técnicas de interpretabilidad en el contexto
de la visión de RL y planteamos una serie de preguntas para futuras
investigaciones.
Nuestro modelo CoinRun
CoinRun es un
juego de plataformas de desplazamiento lateral en el que el agente debe
esquivar enemigos y otras trampas y recoger la moneda al final del nivel.

Nuestro modelo entrenado
jugando CoinRun. Izquierda: resolución completa.
Derecha: observaciones de 64x64 RGB proporcionadas al modelo.
CoinRun se
genera por procedimientos, lo que significa que cada nuevo nivel encontrado por
el agente se genera aleatoriamente desde cero. Esto incentiva al modelo a
aprender cómo detectar los diferentes tipos de objetos en el juego, ya que no
puede salirse con la suya simplemente memorizando una pequeña cantidad de
trayectorias específicas. Usamos la versión original de CoinRun,
no la versión de Procgen Benchmark,
que es ligeramente diferente. Para jugar CoinRun
usted mismo, siga las instrucciones.
A continuación, se muestran
algunos ejemplos de los objetos que se utilizan, junto con las paredes y los
suelos, para generar niveles CoinRun.

I.
El agente, en el aire (izquierda) y a
punto de saltar (derecha). El agente también aparece en beige, azul y verde.
II.
Monedas, que hay que recoger.
III.
Obstáculos estacionarios de sierra
circular, que deben ser esquivados.
IV.
Enemigos, que deben ser esquivados,
moviéndose de izquierda a derecha. Hay varios sprites
alternativos, todos con senderos blancos.
V.
Cajas, sobre las que el agente puede pasar
y aterrizar encima.
VI.
Lava en el fondo de un abismo.
VII.
La información de velocidad pintada en la
parte superior izquierda de cada observación, que indica las velocidades
horizontal y vertical del agente.
Hay 9 acciones disponibles
para el agente en CoinRun:
![]() La
izquierda y la derecha cambian la velocidad horizontal del agente. Todavía
funcionan mientras el agente está en el aire, pero su efecto es menor.
La
izquierda y la derecha cambian la velocidad horizontal del agente. Todavía
funcionan mientras el agente está en el aire, pero su efecto es menor.
![]() Abajo
cancela un salto si se usa inmediatamente después de subir y baja al agente de
las casillas.
Abajo
cancela un salto si se usa inmediatamente después de subir y baja al agente de
las casillas.
![]() Arriba
hace que el agente salte después de la siguiente acción no activa. Las
direcciones diagonales tienen el mismo efecto que las direcciones de ambas
componentes combinadas.
Arriba
hace que el agente salte después de la siguiente acción no activa. Las
direcciones diagonales tienen el mismo efecto que las direcciones de ambas
componentes combinadas.
![]() A, B y
C no hacen nada
A, B y
C no hacen nada
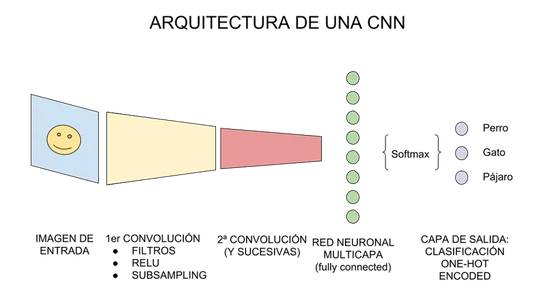
Red neuronal convolucional
Las Redes neuronales convolucionales son
un tipo de redes neuronales artificiales donde
las neuronas corresponden a campos receptivos de una manera muy similar
a las neuronas en la corteza visual primaria (V1) de un cerebro biológico.
Este tipo de red es una variación de un perceptrón multicapa, sin embargo, debido
a que su aplicación es realizada en matrices bidimensionales, son muy efectivas
para tareas de visión artificial, como en la clasificación y
segmentación de imágenes, entre otras aplicaciones.
Cómo están construidas y cómo
funcionan
Las redes
neuronales convolucionales consisten en múltiples capas de filtros
convolucionales de una o más dimensiones. Después de cada capa, por lo general
se añade una función para realizar un mapeo causal no-lineal.
Como cualquier red empleada
para clasificación, al principio estas redes tienen una fase de extracción de
características, compuesta de neuronas convolucionales ,
luego hay una reducción por muestreo y al final tendremos neuronas de
perceptrón más sencillas para realizar la clasificación final sobre las
características extraídas.
La fase de extracción de
características se asemeja al proceso estimulante en las células de la corteza
visual. Esta fase se compone de capas alternas de neuronas convolucionales y
neuronas de reducción de muestreo. Según progresan los datos a lo largo de esta
fase, se disminuye su dimensionalidad, siendo las neuronas en capas lejanas
mucho menos sensibles a perturbaciones en los datos de entrada, pero al mismo
tiempo siendo estas activadas por características cada vez más complejas.
Como se logra que una red
convolucional aprenda
Las Redes neuronales
Convolucionales, CNN aprenden a reconocer una diversidad de objetos dentro de imágenes,
pero para ello necesitan entrenarse de previo con una cantidad importante de
muestras más de 10.000, de ésta forma las neuronas de la red van a poder
captar las características únicas -de cada objeto- y a su vez, poder
generalizarlo a esto es lo que se le conoce como el proceso de aprendizaje
de un algoritmo . Nuestra red va a
poder reconocer por ejemplo un cierto tipo de célula porque ya la ha visto
anteriormente muchas veces, pero no solo buscará celulas
semejantes, sino que podra inferir imagenes que no conozca pero que relaciona y en donde
podrían existir similitudes, y esta es la parte inteligente del reconociminto

Pixeles y neuronas
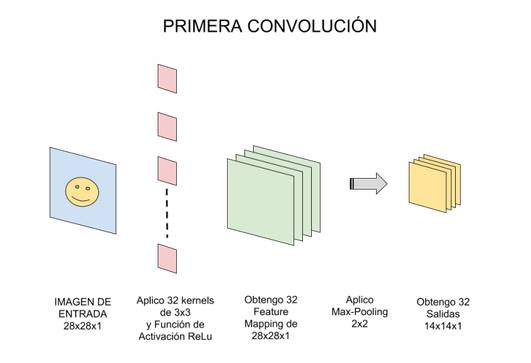
Para comenzar, la red toma
como entrada los pixeles de una imagen. Si tenemos una imagen con apenas 28×28
pixeles de alto y ancho, esTo equivale a utilizar 784
neuronas. Y eso es si sólo tenemos 1 color (escala de grises). Si tuviéramos
una imagen a color, necesitaríamos 3 canales RGB (red, green,
blue) y entonces usaríamos 28x28x3 = 2352 neuronas. Estas neuronas constituyen
nuestra capa de entrada.
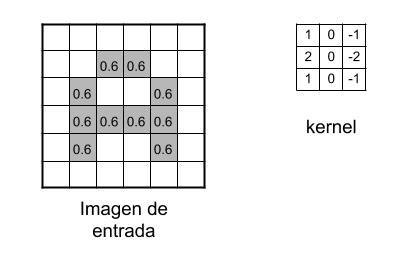
Convoluciones
Ahora comienza el «procesado
distintivo» de las Redes neuronales convolucionales, es decir, haremos las
llamadas convoluciones: Estas consisten en tomar «grupos de pixeles
cercanos» de la imagen de entrada e ir operando matemáticamente
(producto escalar) contra una pequeña matriz que se llama kernel.
Ese kernel supongamos que tiene un tamaño de de 3×3 pixels y con ese tamaño
logra «visualizar» todas las neuronas de entrada (de izquierda-derecha, de
arriba-abajo) y asi logra generar una nueva matriz de
salida, que en definitiva será nuestra nueva capa de neuronas ocultas.
NOTA: si la imagen fuera a
color, el kernel realmente sería de 3x3x3 es decir: un filtro con 3 kernels
de 3×3; luego esos 3 filtros se suman (y se le suma una unidad bias) y conformarán 1 salida (cómo si fuera 1 solo canal).
No aplicaremos 1 sólo kernel, si no que tendremos muchos kernel
(al conjunto de Kernels se les llama filtros). Por
ejemplo en esta primer convolución podríamos tener 32 filtros, con lo cual
realmente obtendremos 32 matrices de salida (este conjunto se conoce como feature mapping), cada una de
28x28x1 dan un total del 25.088 neuronas para nuestra PRIMER CAPA OCULTA de
neuronas, y que solo analiza una imagen cuadrada
de apenas 28 pixeles? Imaginen cuántas más serían si tomáramos una imagen de
entrada de 224x224x3 (que aún es considerado un tamaño pequeño)
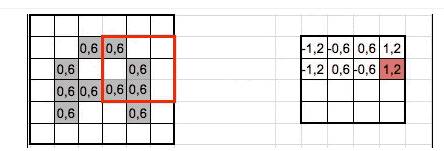
A medida que vamos desplazando el kernel y vamos obteniendo una «nueva imagen» filtrada por
el kernel. En esta primera convolución y
siguiendo con el ejemplo anterior, es como si obtuviéramos 32 «imágenes
filtradas nuevas». Estas imágenes nuevas lo que están «dibujando» son ciertas
características de la imagen original. Esto ayudará en el futuro a poder
distinguir un objeto de otro (por ej. gato ó un
perro).
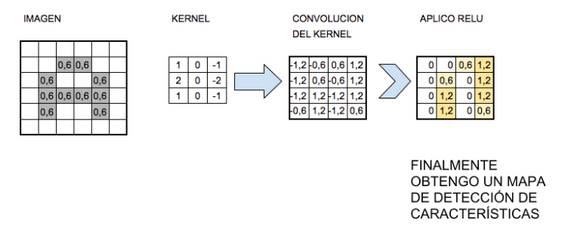
La función de Activación
La función de activación más
utilizada para este tipo de redes neuronales es la llamada ReLu por Rectifier Linear Unit y consiste en una función
f(x)=max(0,x).
La primera convolución es
capaz de detectar características primitivas como lineas
ó curvas. A medida que hagamos más capas con las convoluciones, los
mapas de características serán capaces de reconocer formas más complejas,
y el conjunto total de capas de convoluciones podrá reconocer.
Conectar con una red neuronal tradicional.
Para terminar, tomaremos la
última capa oculta a la que hicimos subsampling, que
se dice que es «tridimensional» por tomar la forma -en nuestro ejemplo- 3x3x128
(alto,ancho,mapas) y la
«aplanamos», esto es que deja de ser tridimensional, y pasa a ser una capa de
neuronas «tradicionales», y con ello aplanamos (y conectamos) una nueva
capa oculta de neuronas tipo feedforward.
Entonces, a esta nueva capa
oculta tradicional, le aplicamos una función llamada Softmax
que conecta contra la capa de salida final que tendrá la cantidad de neuronas
correspondientes con las clases que estamos clasificando. Si clasificamos
perros y gatos, serán 2 neuronas. Si clasificamos coches, aviones
ó barcos serán 3, etc.
Las salidas al momento del
entrenamiento tendrán el formato conocido como one-hot-encoding
en el que para perros y gatos sera: [1,0] y [0,1],
para coches, aviones ó barcos será [1,0,0]; [0,1,0];[0,0,1].
Y la función de Softmax se encarga de pasar a probabilidad (entre 0 y 1) a
las neuronas de salida. Por ejemplo una salida [0,2
0,8] nos indica 20% probabilidades de que sea perro y 80% de que sea gato, segun este ejemplo
Red neuronal convolucional en CoinRun
Entrenamos una red neuronal
convolucional en CoinRun para alrededor de 2 mil
millones de pasos de tiempo, usando PPO, un algoritmo actor-crítico Usamos los
hiperparámetros PPO estándar para CoinRun, excepto
que usamos el doble de copias del entorno por trabajador y el doble y muchos
trabajadores. El efecto de estos cambios fue aumentar el tamaño de lote
efectivo, que parecía ser necesario para alcanzar el mismo rendimiento con
nuestra arquitectura más pequeña. La arquitectura de nuestra red se describe en
el Apéndice C. Usamos una red no recurrente, para evitar la necesidad de
visualizar múltiples cuadros a la vez. Por lo tanto, nuestro modelo observa una
sola imagen de 64x64 con muestreo reducido y genera una función de valor (una
estimación de la recompensa total descontada en el tiempo futuro) y una
política (una distribución de probabilidad sobre las acciones, de la cual se
muestra la siguiente acción).
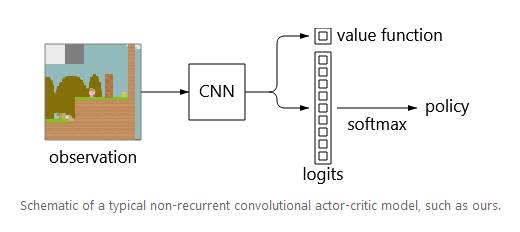
Esquema de un modelo actor-crítico
convolucional no recurrente típico, como el nuestro.
Análisis del modelo
Habiendo entrenado a un fuerte
agente de RL, teníamos curiosidad por ver qué había aprendido. A continuación,
desarrollamos una interfaz para examinar las trayectorias del agente que juega.
Esto incorpora la atribución de una capa oculta que reconoce objetos, que sirve
para resaltar objetos que influyen positiva o negativamente en una salida de
red en particular. Al aplicar la reducción de dimensionalidad, obtenemos
vectores de atribución cuyos componentes corresponden a diferentes tipos de
objeto, los cuales indicamos usando diferentes colores.
Aquí está nuestra interfaz
para una trayectoria típica, con la función de valor como la salida de la red.
Revela el modelo usando obstáculos, monedas, enemigos y más para calcular la
función de valor.
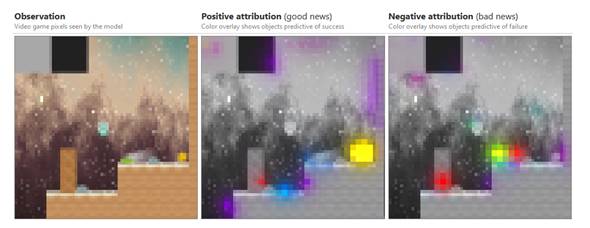
Observación
Píxeles de videojuegos vistos
por el modelo
Atribución positiva
(buenas noticias)
La superposición de colores
muestra objetos que predicen el éxito
Atribución negativa
(malas noticias)
La superposición de colores
muestra objetos que predicen fallas
Leyenda de atribución (coloque
el cursor para aislar)
Los colores corresponden a los
componentes vectoriales después de la reducción de dimensionalidad, los iconos
muestran ejemplos de conjuntos de datos y las etiquetas están compuestas a mano,
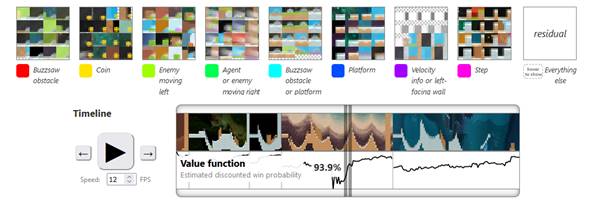
Diseccionando el fracaso
Nuestro modelo totalmente
entrenado no completa alrededor de 1 de cada 200 niveles. Exploramos algunas de
estas fallas utilizando nuestra interfaz y descubrimos que, por lo general,
podíamos comprender por qué ocurrieron.
El fracaso a menudo se reduce
al hecho de que el modelo no tiene memoria y, por lo tanto, debe elegir su
acción basándose únicamente en la observación actual. También es común que
alguna muestra desafortunada de acciones de la política del agente sea en parte
responsable.
Aquí hay algunos ejemplos de
fallas seleccionados cuidadosamente, analizados cuidadosamente paso a paso.



Alucinaciones
Buscamos errores en el modelo
usando estimación de ventaja generalizada (GAE). Usamos los mismos
hiperparámetros GAE que en el entrenamiento, a saber y. que mide el éxito de
cada acción en relación con las expectativas del agente. Un GAE inusualmente
alto o bajo indica que ocurrió algo inesperado o que las expectativas del
agente estaban mal calibradas. El filtrado de dichos intervalos de tiempo
puede, por lo tanto, encontrar problemas con la función o política de valor.
Usando nuestra interfaz,
encontramos un par de casos en los que el modelo "alucinó" una
característica que no estaba presente en la observación, lo que provocó que la
función de valor se disparara.

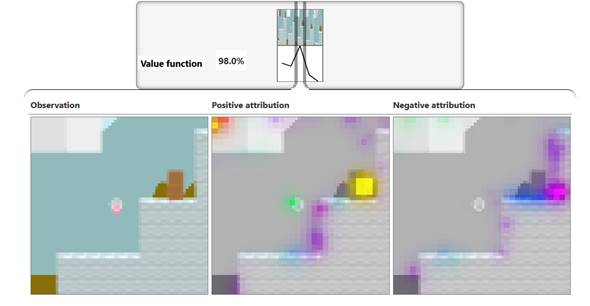

Edición de modelos
Nuestro análisis hasta ahora
ha sido principalmente cualitativo. Para validar cuantitativamente nuestro
análisis, editamos manualmente el modelo para hacer que el agente no vea
ciertas características identificadas por nuestra interfaz: obstáculos de
sierra circular en un caso y enemigos que se mueven hacia la izquierda en otro.
Nuestro método para esto puede considerarse como una forma primitiva de edición
de circuitos, y lo explicamos en detalle en el Apéndice A.
Evaluamos cada edición
midiendo el porcentaje de niveles que el nuevo agente no pudo completar,
desglosados por el objeto con el que el agente colisionó para
causar la falla. Nuestros resultados muestran que nuestras ediciones fueron
exitosas y específicas, sin efectos estadísticamente medibles en las otras
habilidades del agente.
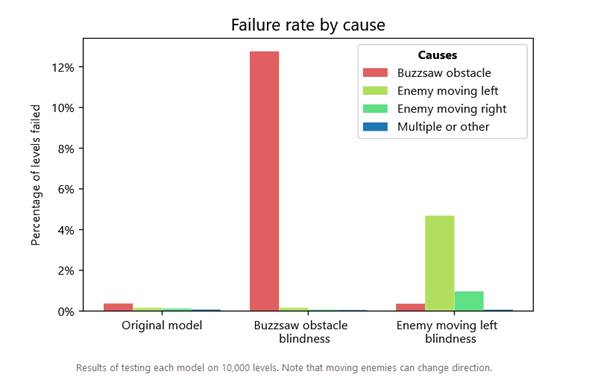
Resultados de probar cada
modelo en 10,000 niveles. Tenga en cuenta que los enemigos en movimiento pueden
cambiar de dirección.
Sin embargo, no logramos
lograr la ceguera total: el modelo editado con sierra circular aún se desempeñó
significativamente mejor que el modelo original cuando hicimos las sierras
completamente invisibles. Nuestros resultados en la versión del juego con
sierras invisibles son los siguientes. niveles fallaron debido a: obstáculo de
la sierra circular / enemigo moviéndose a la izquierda / enemigo moviéndose a
la derecha / múltiple u otro: modelo original, sierras circulares invisibles:
32.20% / 0.05% / 0.05% / 0.05% Probamos el modelo en 10,000 niveles.
Experimentamos brevemente con iteraciones el procedimiento de edición, pero no
pudieron lograr más de alrededor del 50% de ceguera de sierra circular con esta
métrica sin afectar las otras habilidades del modelo. Esto implica que el
modelo tiene otras formas de detectar sierras de zumbido que la característica
identificada por nuestra interfaz.
Aquí están los modelos
originales y editados que juegan algunos niveles seleccionados.
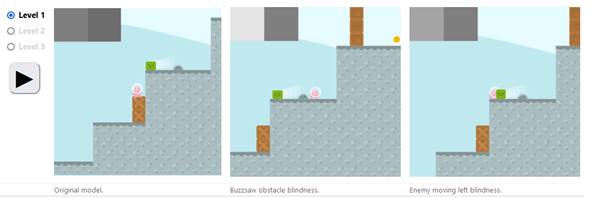

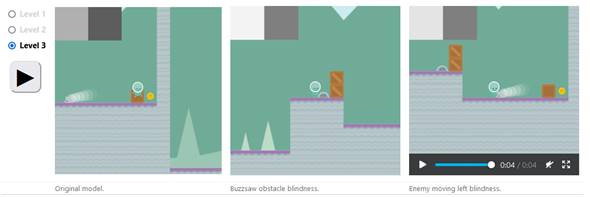
La hipótesis de la diversidad
Todo el análisis anterior
utiliza la misma capa oculta de nuestra red, la tercera de las cinco capas
convolucionales, ya que era mucho más difícil encontrar características
interpretables en otras capas. Curiosamente, el nivel de abstracción en el que
opera esta capa (encontrar las ubicaciones de varios objetos en el juego) es
exactamente el nivel en el que los niveles de CoinRun
se asignan al azar mediante la generación de procedimientos. Además,
descubrimos que el entrenamiento en muchos niveles aleatorios era esencial para
que pudiéramos encontrar cualquier característica interpretable.
Esto nos llevó a sospechar que
la diversidad introducida por la aleatorización de CoinRun
está relacionada con la formación de características interpretables. A esto lo
llamamos la hipótesis de la diversidad:
Las características interpretables tienden
a surgir (en un nivel dado de abstracción) si y solo si la distribución del
entrenamiento es lo suficientemente diversa (en ese nivel de abstracción).
Nuestra explicación de esta
hipótesis es la siguiente. Para la implicación directa ("solo si"),
solo esperamos que las características sean interpretables si son lo
suficientemente generales, y cuando la distribución de entrenamiento no es lo suficientemente
diversa, los modelos no tienen ningún incentivo para desarrollar
características que generalicen en lugar de sobre ajustar. Para la implicación
inversa (si), no esperamos que se cumpla en un sentido estricto: la
diversidad por sí sola no es suficiente para garantizar el desarrollo de
características interpretables, ya que también deben ser relevantes para la
tarea. Más bien, nuestra intención con la implicación inversa es plantear la
hipótesis de que se cumple muy a menudo en la práctica, como resultado de que
la generalización se ve obstaculizada por la diversidad.
En CoinRun,
la generación de procedimientos se usa para incentivar al modelo a aprender
habilidades que se generalizan a niveles invisibles. Sin embargo, solo el
diseño de cada nivel es aleatorio y, en consecuencia, solo pudimos encontrar
características interpretables en el nivel de abstracción de objetos. En un
nivel inferior, solo hay un puñado de patrones visuales en el juego, y las
características de bajo nivel de nuestro modelo parecen consistir
principalmente en configuraciones de color memorizadas que se utilizan para
seleccionarlos. De manera similar, la dinámica de alto nivel del juego sigue
algunas reglas simples y, en consecuencia, las características de alto nivel de
nuestro modelo parecen involucrar mezclas de combinaciones de objetos que son
difíciles de descifrar. Para explorar las otras capas convolucionales, consulte
la interfaz aquí.
Interpretabilidad y
generalización
Para probar nuestra hipótesis,
hicimos que la distribución del entrenamiento fuera menos diversa, al entrenar
al agente en un conjunto fijo de 100 niveles. Esto redujo drásticamente nuestra
capacidad para interpretar las características del modelo. Aquí mostramos una
interfaz para el nuevo modelo, generada de la misma manera que la anterior. La
función de valor que aumenta suavemente sugiere que el modelo ha memorizado el
número de pasos de tiempo hasta el final del nivel y las características que
utiliza para este enfoque en objetos de fondo irrelevantes. Se produce un
sobreajuste similar para otros videojuegos con un número limitado de niveles.
¿ Por que el análisis se realizó sobre la tercer capa?
Resumen y explicación de esta sección
Intentamos cuantificar este
efecto variando el número de niveles utilizados para entrenar al agente y
evaluando las 8 características identificadas por nuestra interfaz sobre cuán
interpretables eran. Se pueden encontrar las interfaces utilizadas para esta
evaluación. Las características se puntuaron en función de la coherencia con la
que se centraran en los mismos objetos y si la atribución de la función de
valor tenía sentido; por ejemplo, los objetos de fondo no deberían ser
relevantes. Este proceso fue subjetivo y ruidoso, pero puede ser inevitable.
También medimos la capacidad de generalización de cada modelo, probando el
agente en niveles invisibles.
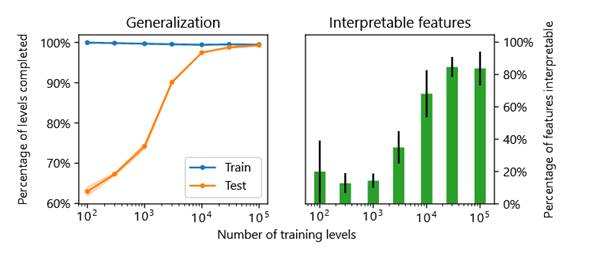
Comparación de modelos
entrenados en diferentes números de niveles. Se entrenaron dos modelos para
cada número de niveles, y dos investigadores evaluaron de forma independiente
cuán interpretables eran las características de cada modelo, sin mostrar el
número de niveles. Nuestra metodología tenía algunas fallas. En primer lugar,
los investigadores no estaban completamente ciegos al número de niveles: por
ejemplo, es posible inferir algo sobre el número de niveles a partir de la suavidad
de los gráficos de la función de valor, ya que con menos niveles el modelo es
más capaz de memorizar el número de pasos de tiempo hasta el final del nivel.
En segundo lugar, dado que las evaluaciones son algo tediosas, las detuvimos
una vez que pensamos que la tendencia se había aclarado, introduciendo cierto
sesgo de selección. Por lo tanto, estos resultados deben considerarse
principalmente ilustrativos. Cada modelo fue probado en 10,000 trenes y 10,000
niveles de prueba muestreados con reemplazo. Las áreas sombreadas en el gráfico
de la izquierda muestran el rango de valores en ambos modelos, aunque en su
mayoría son demasiado estrechos para ser visibles. Las barras de error en el
gráfico de la derecha muestran ± 1 desviación estándar de la población en los
cuatro pares de modelo e investigador.
Nuestros resultados ilustran
cómo la diversidad puede conducir a características interpretables a través de
la generalización, apoyando la hipótesis de la diversidad. Sin embargo, todavía
consideramos que la hipótesis está muy poco probada.
Visualización de características
La visualización de
características responde preguntas sobre lo que buscan determinadas partes de
una red mediante la generación de ejemplos. Esto se puede hacer aplicando un
descenso de gradiente a la imagen de entrada, partiendo de ruido aleatorio, con
el objetivo de activar una neurona o grupo de neuronas en particular. Si bien
este método funciona bien para un clasificador de imágenes entrenado en ImageNet, para nuestro modelo CoinRun
solo produce nubes de color sin rasgos distintivos. Solo para la primera capa,
que calcula convoluciones simples de la entrada, el método produce
visualizaciones comparables para los dos modelos.

Comparación de visualización
de características basada en gradientes para CNN capacitados en ImageNet (GoogLeNet) y en CoinRun (la arquitectura se describe a continuación). Cada
imagen fue elegida para activar una neurona en el centro, con las 3 imágenes
correspondientes a los 3 primeros canales. Se aplicó fluctuación entre los
pasos de optimización de hasta 2 píxeles para la primera capa y hasta 8 píxeles
para la capa intermedia (mixed4a para ImageNet, 2b
para CoinRun).
Se ha demostrado anteriormente
que la visualización de características basada en gradientes tiene problemas
con los modelos RL entrenados en juegos de Atari. Para intentar que funcione
para CoinRun, variamos el método de varias maneras.
Nada de lo que probamos tuvo un efecto notable en la calidad de las
visualizaciones.
·
Robustez de la transformación. Este
es el método de alterar, rotar y escalar estocásticamente la imagen entre los
pasos de optimización, para buscar ejemplos que sean robustos a estas
transformaciones. Intentamos aumentar y disminuir el tamaño del jittering. La rotación y el escalado son menos apropiados
para CoinRun, ya que las observaciones en sí mismas
no son invariantes a estas transformaciones.
·
Penalización de colores extremos. Por
color extremo nos referimos a uno de los 8 colores con valores RGB máximos o
mínimos (negro, blanco, rojo, verde, azul, amarillo, cian y magenta). Al notar
que nuestras visualizaciones tienden a usar colores extremos hacia el medio,
intentamos incluir en el objetivo de visualización una penalización L2 de
varias fortalezas en las activaciones de la primera capa, lo que redujo con
éxito el tamaño de la región de color extremo pero no ayudó de otra manera. .
·
Objetivos alternativos.
Intentamos utilizar un objetivo de optimización alternativo, como el objetivo
de la caricatura. El objetivo de la caricatura es maximizar el producto punto
entre las activaciones de la imagen de entrada y las activaciones de una imagen
de referencia. Las caricaturas son a menudo un tipo de visualización de
características especialmente fácil de hacer que funcione, y útiles para obtener
un primer vistazo de las características que tiene un modelo. Están demostrados
en. Próximamente se publicará un manuscrito más detallado de sus autores.
También intentamos usar la reducción de dimensionalidad, como se describe a
continuación, para elegir direcciones no alineadas con el eje en el espacio de
activación para maximizar.
·
Diversidad visual de bajo nivel. En
un intento por ampliar la distribución de imágenes vistas por el modelo, lo
reentrenamos en una versión del juego con sprites
generados por procedimientos. Además, intentamos agregar ruido a las imágenes,
tanto ruido por píxel independiente como ruido correlacionado espacialmente.
Finalmente, experimentamos brevemente con el entrenamiento contradictorio,
aunque no seguimos muy lejos esta línea de investigación.
Como se muestra a
continuación, pudimos usar ejemplos de conjuntos de datos para identificar una
serie de canales que seleccionan características interpretables por humanos.
Por lo tanto, es sorprendente lo resistentes que fueron a nuestros esfuerzos
los métodos basados en gradientes. Creemos que esto se debe a
que, en última instancia, resolver CoinRun no
requiere mucha habilidad visual. Incluso con nuestras modificaciones, es
posible resolver el juego usando atajos visuales simples, como seleccionar
ciertas configuraciones pequeñas de píxeles. Estos atajos funcionan bien en la
distribución estrecha de imágenes en las que se entrena el modelo, pero se
comportan de manera impredecible en el espacio completo de imágenes en el que
tiene lugar la optimización basada en gradientes.
Nuestro análisis aquí
proporciona una mayor comprensión de la hipótesis de la diversidad. En apoyo de
la hipótesis, tenemos ejemplos de características que son difíciles de
interpretar en ausencia de diversidad. Pero también hay pruebas de que es
posible que sea necesario perfeccionar la hipótesis. En primer lugar, parece
ser una falta de diversidad en un nivel bajo de abstracción lo que daña nuestra
capacidad para interpretar características en todos los niveles de abstracción,
lo que podría deberse al hecho de que la visualización de características
basada en gradientes debe propagarse hacia atrás a través de capas anteriores. . En segundo lugar, el fracaso de nuestros esfuerzos por
aumentar la diversidad visual de bajo nivel sugiere que es posible que la
diversidad deba evaluarse en el contexto de los requisitos de la tarea.
Visualización de
características basada en ejemplos de conjuntos de datos
Como alternativa a la
visualización de características basada en gradientes, usamos ejemplos de
conjuntos de datos. Esta idea tiene una larga historia y se puede considerar
como una forma muy regularizada de visualización de características. Más
detalladamente, tomamos muestras de algunos miles de observaciones del agente
que juega el juego con poca frecuencia y las pasamos a través del modelo. Luego
aplicamos un método de reducción de dimensionalidad conocido como factorización
de matriz no negativa (NMF) a los canales de activación. Más precisamente,
encontramos una factorización de rango bajo aproximada no negativa de la matriz
obtenida al aplanar las dimensiones espaciales de las activaciones en la
dimensión del lote. Esta matriz tiene una fila por observación y una columna
por canal: por lo tanto, la reducción de dimensionalidad no utiliza información
espacial. Para cada uno de los canales resultantes (que corresponden a
combinaciones ponderadas de los canales originales), elegimos las observaciones
y posiciones espaciales con la activación más fuerte (con un número limitado de
ejemplos por posición, para diversidad), y mostramos un parche de la
observación. en esa posición.


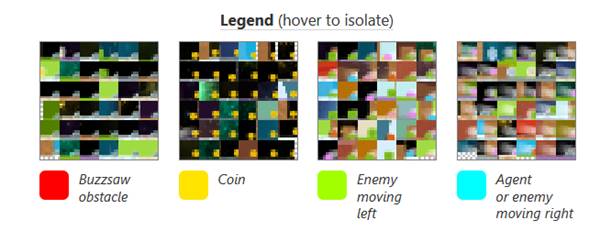
Visualizaciones de
características basadas en ejemplos de conjuntos de datos para 16 direcciones
NMF de la capa 2b de nuestro modelo CoinRun. El
tablero de ajedrez gris-blanco representa el borde de la pantalla. Las
etiquetas están compuestas a mano.
A diferencia de la
visualización de características basada en gradientes, este método encuentra
algún significado para las diferentes direcciones en el espacio de activación.
Sin embargo, es posible que aún no proporcione una imagen completa para cada
dirección, ya que solo muestra un número limitado de ejemplos de conjuntos de datos
y con un contexto limitado.
Visualización de
características con reconocimiento espacial
Las observaciones de CoinRun se diferencian de las imágenes naturales en que son
mucho menos invariantes espacialmente. Por ejemplo, el agente siempre aparece
en el centro y la velocidad del agente siempre se codifica en la parte superior
izquierda. Como resultado, algunas características detectan cosas no
relacionadas en diferentes posiciones espaciales, como leer la velocidad del
agente en la parte superior izquierda mientras detectan un objeto no
relacionado en otra parte. Para dar cuenta de esto, desarrollamos una versión
espacialmente consciente de la visualización de características basada en
ejemplos de conjuntos de datos, en la que arreglamos cada posición espacial a
su vez, y elegimos la observación con la activación más fuerte en esa posición
(con un número limitado de reutilizaciones de la misma observación, para la
diversidad). Esto crea una correspondencia espacial entre visualizaciones y
observaciones.
Aquí hay una visualización de
este tipo para una función que responde fuertemente a las monedas. Los
cuadrados blancos en la parte superior izquierda muestran que la característica
también responde fuertemente a la información de velocidad horizontal cuando es
blanca, lo que corresponde al agente que se mueve hacia la derecha a toda
velocidad.

Visualización de
características basadas en ejemplos de conjuntos de datos con reconocimiento
espacial para la dirección NMF de detección de monedas de la capa 2b. La
transparencia (que revela el fondo con rayas diagonales) indica una respuesta
débil, por lo que la mitad izquierda de la visualización es mayormente
transparente porque las monedas nunca aparecen en la mitad izquierda de las
observaciones.
Atribución
La atribución responde
preguntas sobre las relaciones entre neuronas. Se usa más comúnmente para ver
cómo la entrada a una red afecta una salida en particular, por ejemplo, en RL,
pero también se puede aplicar a las activaciones de capas ocultas. Aunque hay
muchos enfoques de atribución que podríamos haber utilizado, elegimos el método
de gradientes integrados. En el Apéndice B explicamos cómo aplicamos este
método a una capa oculta y cómo la atribución de función de valor positivo
puede considerarse como "buenas noticias" y la atribución de función
de valor negativo como "mala noticia".
Reducción de dimensionalidad
para atribución
Demostramos anteriormente que
un método de reducción de dimensionalidad conocido como factorización de matriz
no negativa (NMF) podría aplicarse a los canales de activaciones para producir
direcciones significativas en el espacio de activación. Descubrimos que es aún
más efectivo aplicar NMF no a activaciones, sino a atribuciones de funciones de
valor Como antes, obtenemos las direcciones de NMF muestreando algunos miles de
observaciones con poca frecuencia del agente que juega el juego, calculando las
atribuciones, aplanando las dimensiones espaciales en la dimensión del lote y
aplicando NMF. (Trabajando alrededor del hecho de que NMF solo se puede aplicar
a matrices no negativas Nuestra solución es separar las partes positivas y
negativas de las atribuciones y concatenarlas a lo largo de la dimensión del
lote. También podríamos haberlas concatenado a lo largo de la dimensión del
canal). Ambos métodos tienden a producir direcciones NMF cercanas a one-hot, por lo que se puede pensar que seleccionan los
canales más relevantes. Sin embargo, cuando se reduce a un pequeño número de
dimensiones, el uso de atribuciones suele seleccionar características más
destacadas, porque la atribución tiene en cuenta no solo a qué responden las
neuronas, sino también si su respuesta es importante.
A continuación, después de
aplicar NMF a las atribuciones, las visualizamos asignando un color diferente a
cada uno de los canales resultantes. Superponemos estas visualizaciones sobre
la observación y contextualizamos cada canal mediante la visualización de
características, haciendo uso de la visualización de características basada en
ejemplos de conjuntos de datos. Esto da una versión básica de nuestra interfaz,
que nos permite ver el efecto de las características principales en diferentes
posiciones espaciales.

Atribución de función de valor
para una observación seleccionada con precisión utilizando la capa 2b de
nuestro modelo CoinRun, reducida a 4 canales
utilizando NMF basado en atribución. Las visualizaciones de características
basadas en ejemplos de conjuntos de datos de estas direcciones revelan
características más destacadas que las visualizaciones de las primeras 4
direcciones NMF basadas en activación de la sección anterior.
Para la versión completa de
nuestra interfaz, simplemente repetimos esto para una trayectoria completa del
agente que juega el juego. También incorporamos controles de video, una vista
de línea de tiempo de observaciones comprimidas e información adicional, como
resultados de modelos y acciones de muestra. Juntos, permiten que la
trayectoria se explore y se comprenda fácilmente.
Discusión de atribución
Las atribuciones para nuestro
modelo CoinRun tienen algunas propiedades
interesantes que serían inusuales para un modelo ImageNet.
·
Escasez. La atribución tiende a
concentrarse en un número muy pequeño de posiciones espaciales y canales
(post-NMF). Por ejemplo, en la figura anterior, los 10 pares de canal y
posición principales representan más del 80% de la atribución absoluta total.
Esto podría explicarse por nuestra hipótesis anterior de que el modelo
identifica objetos seleccionando ciertas configuraciones pequeñas de píxeles.
Debido a esta escasez, suavizamos la atribución sobre posiciones espaciales
cercanas para la versión completa de nuestra interfaz, de modo que la cantidad
de espacio visual ocupado se pueda usar para juzgar la fuerza de la atribución.
Esto intercambia algo de precisión espacial por más precisión con magnitudes.
·
Signo inesperado. La
atribución de función de valor generalmente tiene el signo que uno esperaría:
positivo para monedas, negativo para enemigos, etc. Sin embargo, a veces este
no es el caso. Por ejemplo, en la figura anterior, el canal rojo que detecta
los obstáculos de la sierra circular tiene una atribución tanto positiva como
negativa en dos posiciones espaciales vecinas hacia la izquierda. Nuestra mejor
suposición es que este fenómeno es el resultado de la colinealidad estadística,
causada por ciertas correlaciones en la generación del nivel procedimental
junto con el comportamiento del agente. Estos pueden ser visuales, como
correlaciones entre píxeles cercanos, o más abstractos, como monedas y paredes
largas que aparecen al final de cada nivel. Como ejemplo de juguete, suponiendo
que la función de valor debería aumentar en un 2% cuando el final del nivel sea
visible, el modelo podría aumentar la función de valor en un 1% para monedas y
un 1% para paredes largas, o en un 3% para monedas. y -1% para paredes largas,
y el efecto sería similar.
·
Marcos de valores atípicos.
Cuando un evento inusual hace que la red genere valores extremos, la atribución
puede comportarse de manera especialmente extraña. Por ejemplo, en el marco de
la alucinación de la sierra circular, la mayoría de las características tienen
una cantidad significativa de atribución tanto positiva como negativa. No
tenemos una buena explicación para esto, pero quizás las características
interactúan de formas más complicadas de lo habitual. Además, en estos casos, a
menudo hay un componente significativo de la atribución que se encuentra fuera
del espacio abarcado por las direcciones NMF, que mostramos como una
característica "residual" adicional. Esto podría deberse a que cada
cuadro se pondera por igual cuando se calcula NMF, por lo que los cuadros
atípicos tienen poca influencia sobre las direcciones de NMF.
Estas consideraciones sugieren
que se puede requerir cierto cuidado al interpretar las atribuciones.